Antipresbiterio centrale
Il piano dell'Antipresbiterio
In questa sezione: Compensazioni interstiziali e deformate - Rapporto di quadratura mosaico-marmo - Scrittura a sintassi circolare e cartesiana- Campi biquadratici nucleati- Campi mono- e biassiali - Brani angolari standard - Procedimenti di curvatura del modulo
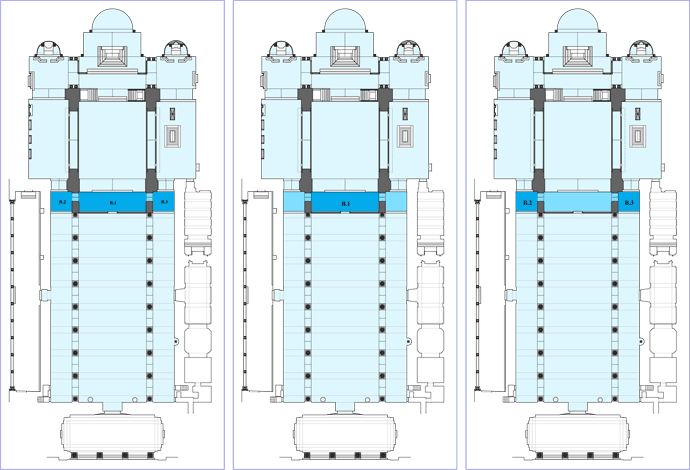
Fig. __. Da sinistra a destra: Piano dell'Antipresbiterio [B.1 B.2 B.3]; Campata centrale dell'Antipresbiterio o Atrio del Coro [B.1]; Campata laterale sinistra dell'Antipresbiterio [B.2]; Campata laterale destra dell'Antipresbiterio [B.3].
Campata Centrale dell'Antipresbiterio o Atrio del Coro
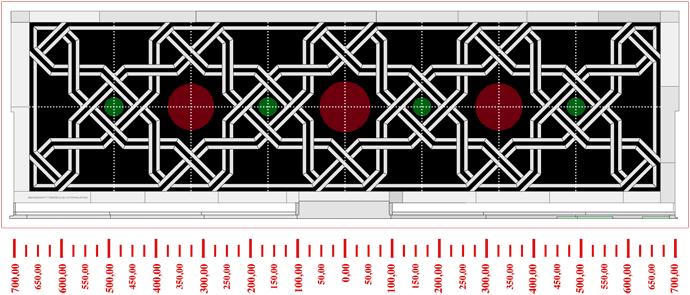
Figura. La campitura in nero, corrispondente alle zone in mosaico, mette in risalto il disegno marmoreo della trama. Sull'asse trasversale del settore si susseguono dischi di porfido e serpentino, posti al centro di campi di tipo biquadratico e a losanga.
Dal punto di vista cronologico, il settore pavimentale dell'Atrio del Coro è quello di più recente esecuzione [1915]. Sul suo bordo marmoreo, in prossimità della transenna che lo separa dall'aula ecclesiale, sono incise due epigrafi, contenenti, rispettivamente, l'indicazione dell'anno d'esecuzione dell'opera e quella dei maestri marmorari che l'hanno eseguita. Perfetto lo stato di conservazione, non solo perché l'opera è di recente esecuzione, ma per essere normalmente esclusa al transito dei visitatori. Sotto il profilo iconografico, il settore si compone di tre unità biquadratiche [E1, E2, E3], del tipo nucleato [con nucleo circolare in posizione centrale], accostate trasversalmente e intervallate da strutture intermodulari a losanga, anch'esse di tipo nucleato [B1, B2, B3, B4].
Epigrafe n. 1 [angolo nord-ovest]: IOS. MATRANGA.ET.PETR.REGINELLA.MARMORARIIS; Epigrafe n. 2 [angolo sud-ovest]: ANNO.DOMINI.MCMXV - A.QUINQUE.VIRIS.TEMPLO.INSTAURANDO - DOMINICO.GASPARE.LANCEA.ARCHIEP. - OPUS.MUSIVUM.EX.INTEGRO.FACTUM.]

Figura. Nella stesura musiva dei campi biquadratici emergono le tre diverse modalità di scrittura delle composizioni.
Tre le modalità di redazione dei testi inseriti negli spazi tra la sagoma biquadratica e il nucleo. Nella prima modalità, il testo, correlandosi al nucleo circolare, fluisce intorno ad esso, dilatandosi radialmente con continuità e progressione [E1]; nella seconda, rapportandosi ai lati retti della sagoma biquadratica, si dispone parallelamente al suo perimetro [E2]; nella terza, combinando le due modalità precedenti, si sviluppa, in parte parallelamente ai lati della sagoma [rapporto alla sagoma biquadratica], in parte attorno al disco di porfido assecondandone la curvatura [rapporto alla sagoma nucleare] [E3].
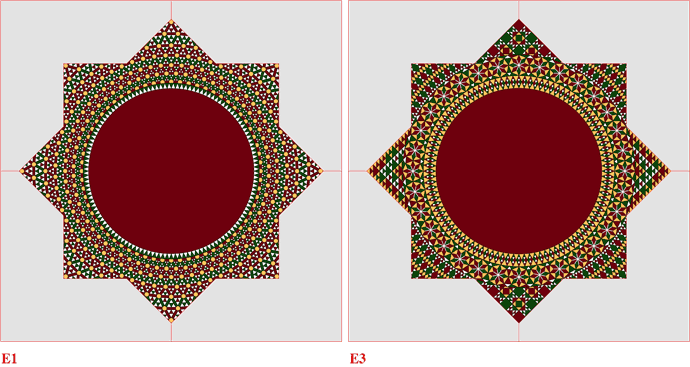
Figura. Il modulo E1 costituisce un esempio di scrittura a sintassi circolare, con progressiva dilatazione radiale del testo. Il modulo E3 è, al contrario, un esempio di scrittura mista, riunendo la modalità di scrittura a sintassi circolare [cantoni angolari] con quella a sintassi cartesiana [cantoni assiali]. Diametro dei dischi di porfido oscillante tra 99 e 108 cm.

Figura. Procedendo dal centro alla periferia del campo biquadratico, il motivo esagonale subisce una dilatazione progressiva e continua.

Figura. La doppia cerchiatura attorno al disco di porfido, dal suo perimetro agli angoli interni della sagoma biquadratica, determina la suddivisione del campo residuo in otto settori [cantoni] di forma triangolare mistilinea, in ciascuno dei quali si alternano brani a tessitura retta e brani a tessitura curva.
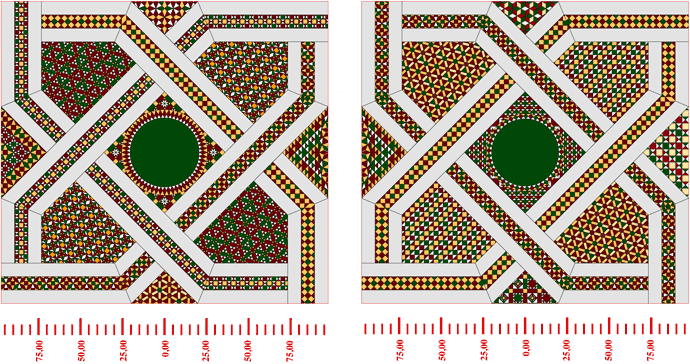
Figura. Campi musivi a losanga con nucleo circolare al centro [B3, B4]. Dischi di serpentino con diametro variabile dai 45 ai 60 cm [circa metà dei dischi di porfido].
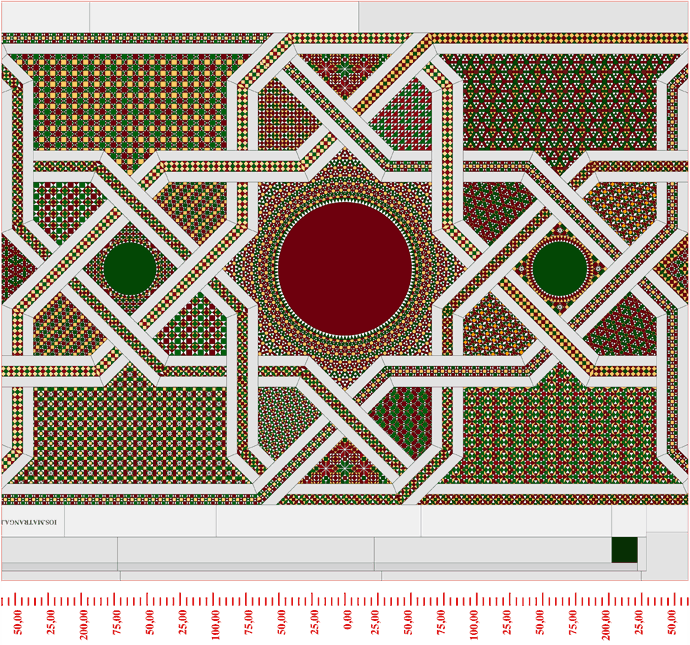
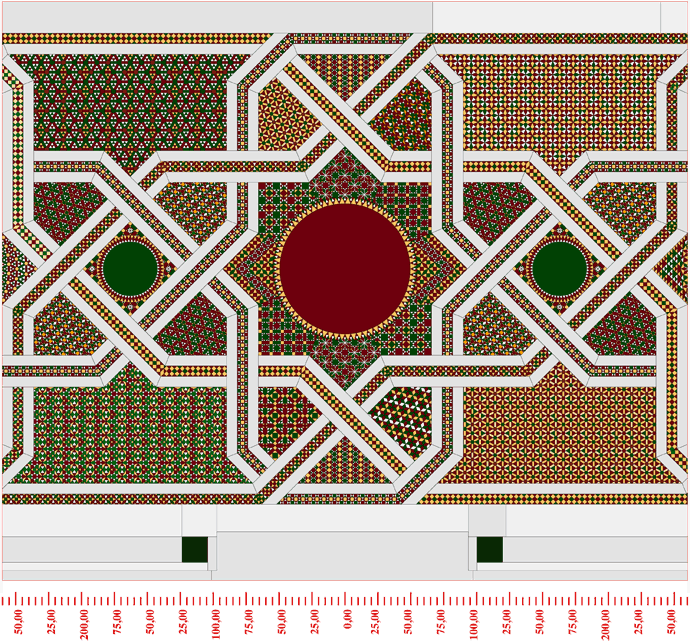
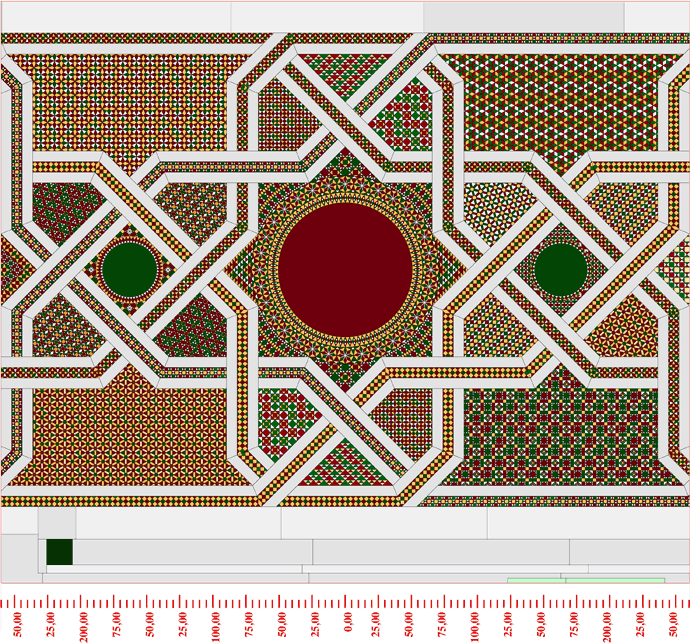
Figura. Moduli n.1, n.2 e n.3 [la numerazione va da sinistra a destra]. Sotto il profilo figurativo, i moduli si compongono di strutture biquadratiche del tipo nucleato. La grandezza dei dischi oscilla dai 99 ai 108 cm.

[Foto G. Oddo - Luglio 2009]
Iconografia dell'impianto
![]()
Figura. Diagramma iconografico. A fornire l'impianto figurativo di un testo è il complesso delle tracce che, evolvendosi nel campo come nervature di una crociera gotica, e variamente intrecciandosi, compongono ciò che definiamo trama.
Un diagramma iconografico individua i percorsi delle singole tracce, distinguendoli, cromaticamente, l'uno dall'altro, in modo da rendere evidente la dinamica di ciascuno e la struttura dell'impianto iconografico globale. In generale, considerandone l'evoluzione, una traccia può attraversare il campo figurativo e simulare la prosecuzione al di là dei suoi limiti, o evolversi tutta al suo interno, chiudendosi ad anello dopo un percorso più o meno intricato. Poiché a ogni traccia corrisponde un particolare ed esclusivo modulo figurativo, per la scrittura dei testi in essa contenuti, la differenziazione cromatica, oltre ad individuare e mettere in risalto la pluralità delle tracce, individua e mette in risalto anche il numero e la varietà delle tipologie.
![]()
Figura. A sinistra: Traccia anulare a sviluppo simmetrico - A destra: Traccia anulare a sviluppo dissimmetrico. Le tracce a sviluppo dissimmetrico sono generalmente usate in combinazione con altre di tracciato complementare, così da ricostituire, assieme, la simmetria dell'impianto iconografico.
Campi musivi mono- e biassiali
Qualunque dispositivo modulare, proprio in quanto modulare, ha un'attitudine strutturale ad aggregarsi in più direzioni del piano, ricoprendolo in modo più o meno compatto. Nelle nostre applicazioni, il modulo è usato, sia in composizioni di tipo lineare, dette monoassiali, sia in composizioni di tipo superficiale, dette biassiali. L'aggettivazione mono- e biassiale, usata in rapporto alle modalità di aggregazione dei moduli e alla composizione dei testi, può estendersi a denotare l'attitudine degli alvei alla ricettività di stesure del primo o del secondo tipo. Avremo, pertanto, campi di tipo monoassiale e campi di tipo biassiale.
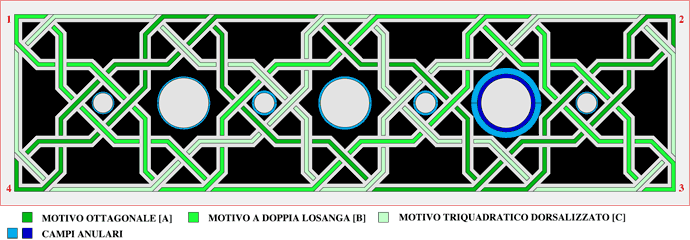
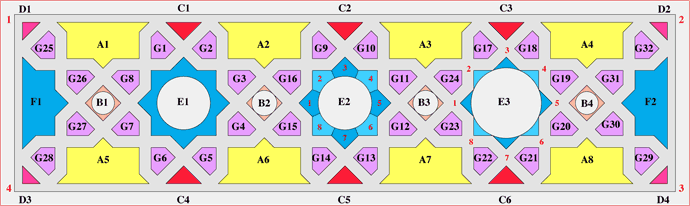
Figura. Sopra. Campi musivi di tipo lineare o monoassiale. Il decorso dei campi monoassiali può essere rettilineo o circolare. Le problematiche del decorso rettilineo riguardano la spezzatura del modulo in corrispondenza delle piegature della stecca; le problematiche del decorso curvilineo riguardano i procedimenti di curvatura del modulo. Sotto. Campi musivi biassiali. Le sigle a doppio indice contengono l'indicazione della tipologia [sagoma] dell'alveo e della posizione dell'unità.
Quadratura dei campi musivi
La quadratura dei campi musivi non serve solo a rilevare il dato assoluto di estensione della superficie in mosaico, ma ad elaborare un indice di consistenza della componente musiva in rapporto alla componente marmorea. Serve, in sostanza, a valutare la prevalenza proporzionale di una componente sull'altra, l'entità di scavo della crosta marmorea [impianti a lastratura continua], o la consistenza di apporto, del marmo, nella costituzione dell'ossatura pavimentale [impianti a lastratura discontinua]. Gli indici introdotti riguardano: l'incidenza percentuale sul totale di quadratura del campo e il rapporto di quadratura mosaico-marmo. Il rapporto di quadratura mosaico-marmo misura l'ordine di molteplicità del mosaico sul marmo. Nel caso del settore n.3, l'ordine di molteplicità è prossimo a 2 e 1/4, il che vuol dire che la superficie musiva ha un'estensione più che doppia rispetto alla superficie marmorea.
Quadratura dei Campi biassiali
Campi di tipo A: mq 1,15; in totale, A1-A8, mq 9,20
Campi di tipo B: B1 mq 0,09 - B2 mq 0,06 - B3 mq 0,06 - B4 mq 0,09; in totale mq 0,30
Campi di tipo C: mq 0,13; in totale, C1-C6, mq 0,78
Campi di tipo D: mq 0,65; in totale, D1-D4, mq 2,60
Campi di tipo E: E1 mq 1,12 - E2 mq 1,11 - E3 mq 0,44; in totale mq 2,67 Campi di tipo F: mq 1,01; in totale, F1-F2, mq 2,02
Campi di tipo G: mq 0,18; in totale, G1-G32, mq 5,76
Sommano mq 23,33 pari al 48,78 % dell'area del settore
Quadratura dei Campi monoassiali
Nastro tipologia A [motivo esagonale]: mq 2,79
Nastro tipologia B [motivo a doppia losanga]: mq 2,79
Nastro tipologia C [motivo triquadratico dorsalizzato]: mq 2,87
Anelli B1 B4: mq 0,08
Anelli B2 B3: mq 0,14
Anello E1: mq 0,11
Anello E2: mq 0,15
Anello E3 interno: mq 0,26
Anello E3 esterno: mq 0,52
Sommano mq 9,71 pari al 20,30 % dell'area del settore
- Area del settore 3 [vertici 1-4]: mq 47,83
- Totale area musiva mq 33,04 pari al 69,08 % dell'area del settore
- Totale area marmorea mq 14,79 pari al 30,92 % dell'area del settore
- Rapporto di quadratura mosaico marmo 33,04/14,79 = 2,23
Tipologie figurative biassiali
Le tipologie modulari hanno un'attitudine intrinseca a declinarsi in forma di strutture biassiali, estendendosi nel piano e ricoprendolo con continuità. L'impiego di una tipologia in senso monoassiale può implicare parziali ritocchi al suo contorno, specialmente quando la tipologia, per sua natura, manca di una propria strutturale squadratura, almeno, bilaterale [squadratura della tipologia]. L'adattamento consiste nello tranciatura di quelle eccedenze dei dispositivi, inutilizzati come congegni di connessione. In questo paragrafo, ci soffermeremo unicamente sugli episodi di declinazione biassiale delle tipologie e ne considereremo il numero e le dislocazioni.
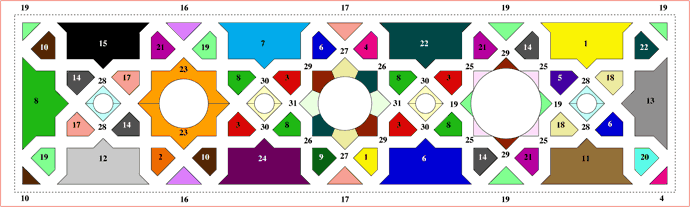
Figura. A ciascun motivo figurativo è associato un determinato colore o una sfumatura di colore. In tali abbinamenti, e nella contiguità di un colore con un altro, non c'è una logica di classificazione delle tipologie: una tonalità più chiara e una più scura non indicano, pertanto, rapporti di derivazione da comuni ceppi figurativi.

Figura.

Figura.

Figura.

Figura.
Tipologie figurative monoassiali

Figura. A B e C sono usate nella redazione di composizioni a decorso rettilineo; D E F G H e I nella redazione di composizioni a decorso circolare.
Compensazioni interstiziali, morfologiche e da sottodimensionamento
I problemi delle composizioni lineari sono di due tipi: in quelle a decorso rettilineo, è problematico il taglio dei moduli, nei punti di piegatura delle tracce, per effetto della spezzatura direzionale del testo; in quelle a decorso circolare, è l'incurvatura stessa degli elementi del modulo a determinare la problematicità del procedimento. Operativa ed empirica la risoluzione del primo tipo di problemi; tecnicamente più raffinata e complessa quella del secondo.
Nell'ambito delle modalità di trattamento delle problematiche del primo tipo, le soluzioni del settore n. 3 costituiscono i risultati esecutivamente più evoluti. La particolarità di tali soluzioni si basa sulla preventiva definizione di brani angolari standard [grafici B1 C1 D1 e B2 C2 D2].
La definizione di brani angolaristandard implica, necessariamente, che decorra da tali punti [piegatura delle tracce] la stesura dell'impianto musivo. Procedendo verso il centro della stecca, l'eventuale impossibilità di chiudere l'enunciato, con l'inserimento di un modulo intero, verrebbe artificiosamente compensata, o agendo sul valore degli interstizi [sistema delle compensazioni interstiziali], o modificando la dimensione longitudinale del modulo [sistema delle compensazioni deformate].
I procedimenti descritti costituiscono le modalità comunemente impiegate in campo digitale, per la facilità, in esso, di gestire aspetti relativi alla riscalatura o alla spaziatura degli elementi compositivi.
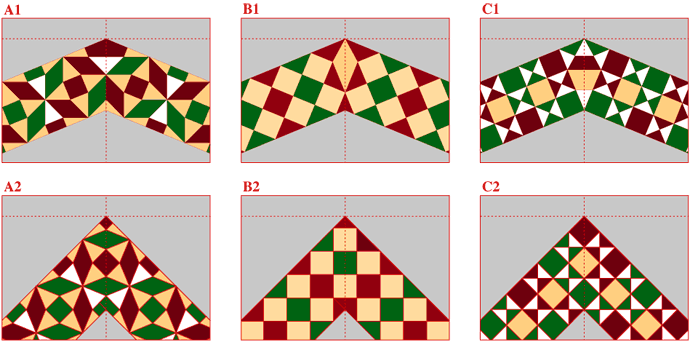
Figura. Soluzioni d'angolo. Sopra [A1 B1 C1]: piegature a 135°. Sotto [A2 B2 C2]: piegature a 90°. Il caso della fig. C2 ha valore esclusivamente teorico perché, nel decorso della relativa fascia, non si verificano piegature ad angolo retto.
Si può dire, dunque, che: in un procedimento di standardizzazione delle soluzioni d'angolo, la stesura del testo musivo procede, obbligatoriamente, dalle estremità verso il centro della stecca. Sotto il profilo compositivo, la situazione ideale è che lo spazio del testo contenga, esattamente, un numero intero di moduli. Se ciò non si verifica, se dopo le aggregazioni intere dovesse ancora avanzare uno spazio residuo [fig. A], sia in ambito digitale che reale, i procedimenti di risoluzione impiegati si basano o sulla compensazione interstiziale [fig. C], per cui si modifica l'entità degli interstizi tra le formelle della stecca, o sulla deformazione longitudinale [fig. D], per cui si interviene sulla lunghezza del modulo, dilatandone o contraendone il valore.
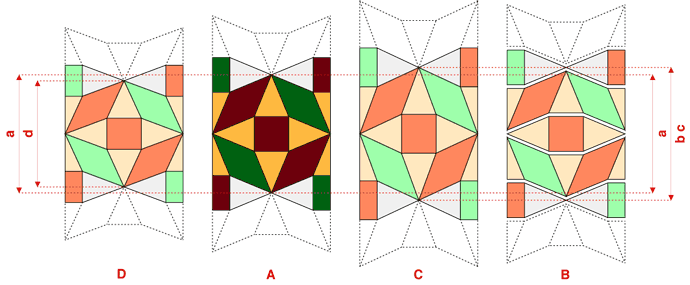
Figura. A: soluzione standard.B C D: soluzioni compensate. In C e D la compensazione è per deformazione del modulo, allungando [c] o riducendo [d] il passo modulare standard [a]; in B per dilatazione interstiziale.
Nelle nostre considerazioni, per ovvie ragioni operative, domina il riferimento all'esperienza dei procedimenti digitali, che, come abbiamo detto, e come può, d'altra parte, facilmente arguirsi, differiscono solo in parte da quelli puramente manuali, non fosse che per quel nesso di continuità tra teorico e pratico, che attribuisce al primo una funzione prefigurativa, immune dalle accidentalità esecutive.
Così, ad esempio, in ambito digitale è assoluta l'identità tra dimensione nominale e dimensione rappresentativa dell'opera [per cui, un brano musivo assume identica larghezza dell'incàvo marmoreo cui è destinato], è costante ed uniforme il passo modulare, ed è perfetta la scrittura lessicale e sintattica della frase. Gli stessi risultati non si riscontrano sul piano della materiale esecuzione dell'opera. L'identità delle misure è sacrificata all'esigenza di sottodimensionare il testo, per renderne agevole l'inserimento nell'alveo; l'uniformità del passo modulare è una condizione attuabile solo approssimativamente; approssimativa, inevitabilmente, è anche la forma dei singoli elementi [lessico] e degli aggregati [fraseologia] che essi compongono.
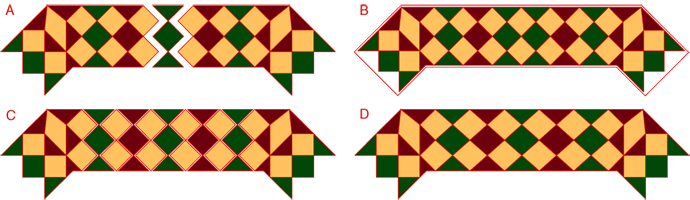
Figura. A: spazio residuo sottomodulare. B: inserimento sottodimensionato. C: compensazione interstiziale. D: compensazione per deformazione longitudinale.
Adattamento curvilineo del motivo della stella a otto punte [e non solo]
Sull'argomento si torna nella sezione "Antipresbiterio DX".
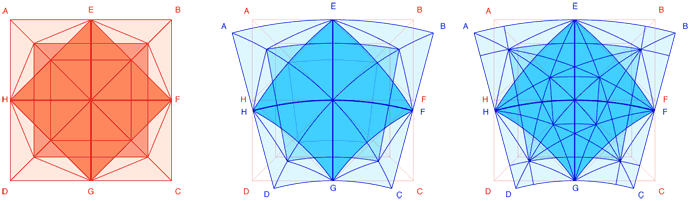
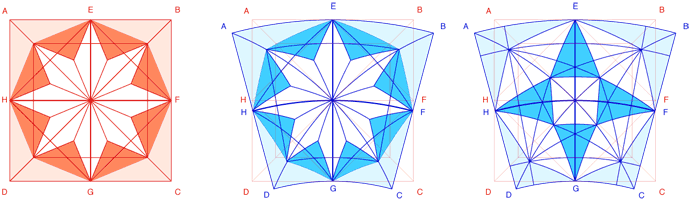
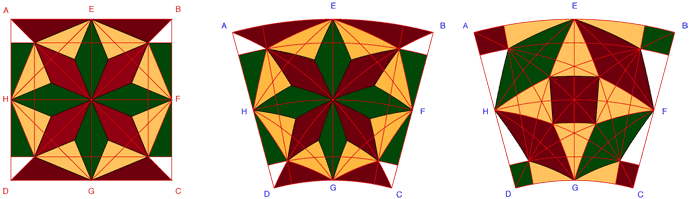
Figura. I disegni mostrano il procedimento teorico di conversione, in senso circolare, dei motivi della stella a otto punte ed ottagonale. Sul piano esecutivo, la curvatura dei lati è sostituita dalla corda ad essi sottesa.
Al di là delle problematiche di curvatura del modulo e delle modalità di effettiva esecuzione, quali altri aspetti esigono, da parte di chi opera, il possesso di più raffinate competenze teoriche?
Considerando il modulo nel suo astratto isolamento [aseità], ne abbiamo appena, visivamente, descritto gli effetti deformanti della curvatura sui singoli elementi che lo costituiscono e sull'insieme figurativo che essi compongono. Ci soffermeremo, adesso, a considerare le circostanze pratiche d'impiego del modulo, in rapporto ad un'esigenza reale, alla quale esso deve, necessariamente e flessibilmente, adattarsi, assumendo precise dimensioni e correlandosi alla grandezza di un campo circolare, secondo un calcolato effetto d'impatto visivo.
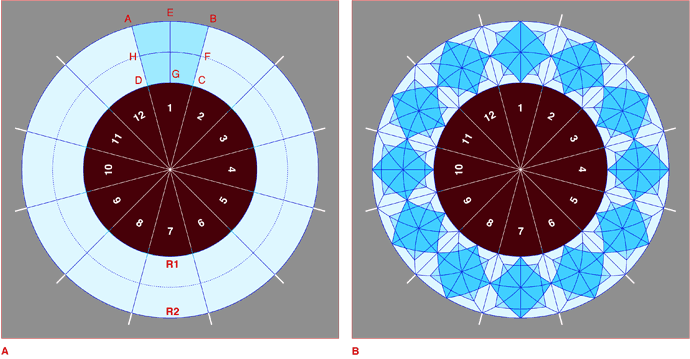
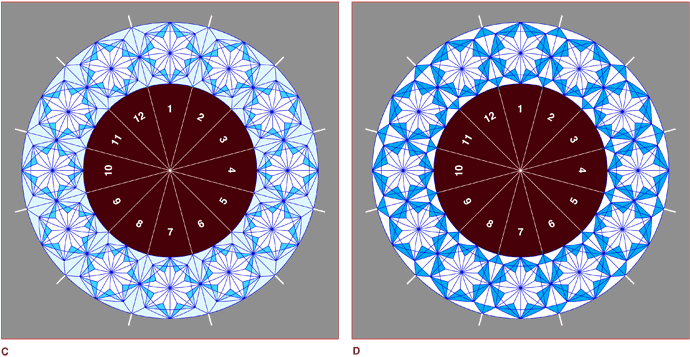
Figura. A e B: il primo adempimento procedurale è la suddivisione della circonferenza in un numero intero di parti, tante quanti sono i moduli; l'adempimento successivo consiste nella determinazione della sagoma d'inviluppo del modulo e nell'inserimento, al suo interno, del dispositivo biquadratico. C e D: sullo schema tracciato nella fase B si costruisce la stella a otto punte e i relativi brani che completano la formulazione del modulo.
Nell'elaborazione di una cerchiatura ad elementi modulari, il primo adempimento è di suddividere la circonferenza in un numero "n" di parti, uguale al numero di moduli che si vuole aggregarvi attorno. Nell'esempio, figura A, la circonferenza è stata suddivisa in 12 parti, ciascuno di lunghezza uguale all'arco C-D, che costituisce, nello svilupppo dell'elaborazione, la base di un quadrato deformato [A-B-C-D], al cui interno s'inscrive lo schema biquadratico della stella a otto punte. Ma per completare il disegno del quadrato, occorreranno altri due dati: la misura dell'altezza E-G e quella della larghezza H-F.
Dalla relazione E-G = H-F, tenendo conto che nella curvatura del quadrato, l'altezza E-G e la larghezza media H-F mantengono le loro reali dimensioni [mentre il lato interno C-D si contrae e il lato esterno A-B si dilata], indicando con R1 e R2 il raggio dell'arco interno C-D [R minore] e quello dell'arco esterno A-B [R maggiore], si ricava un'equazionerisolutiva, ossia un'equazione dalla quale attingere il valore del raggio della circonferenza esterna d'inviluppo:
R2-R1 = π(R1+R2)/n
R2 = [(n+π)/(n-π)]R1.
La lunghezza dell'arco interno C-D si ottiene dalla formula: C-D = (2πR1)/n; quella dell'arco esterno, da A-B = (2πR2)/n.

